이진 탐색 = 이분 탐색 (Binary Search)
정렬된 배열 또는 리스트에 적합한 고속 탐색 방법이다.
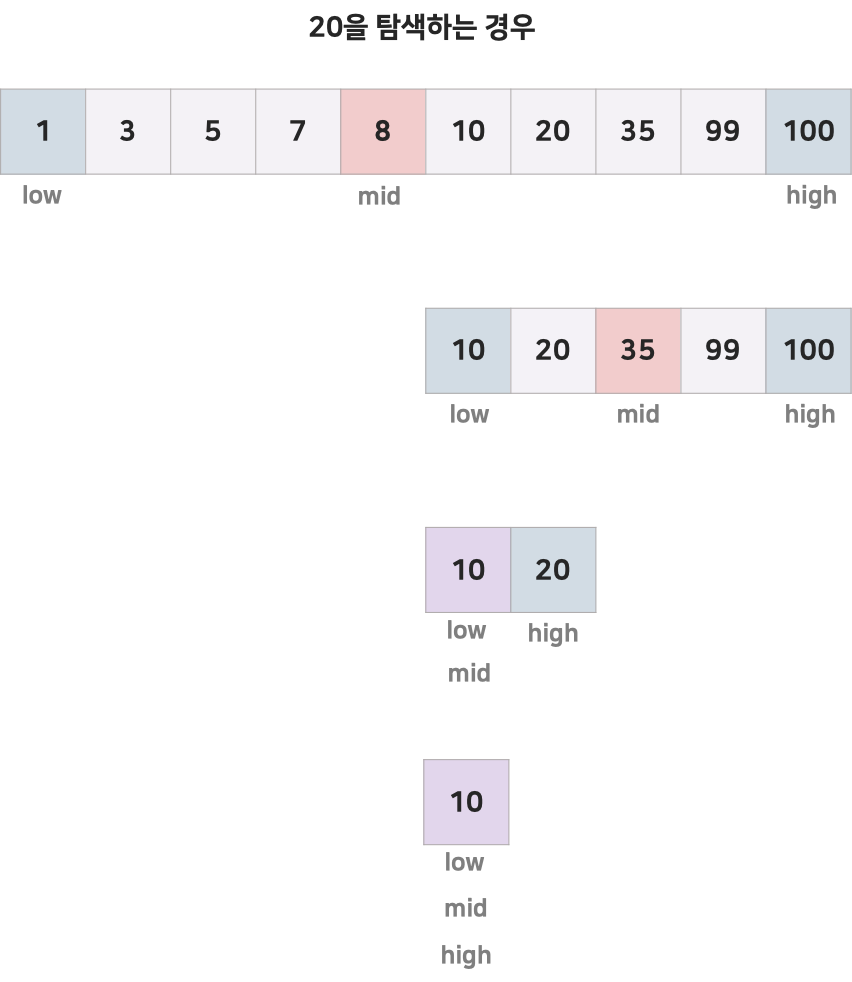
- 배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄인다.
- 찾고자 하는 값이 속해있지 않은 부분은 전혀 고려할 필요가 없기 때문에, 매 단계에서 검색해야 할 리스트의 크기를 반으로 줄일 수 있다.
- 이러한 방법을 반복적으로 사용해 탐색하는 방법이 이진 탐색이다.
- 데이터의 삽입이나 삭제가 빈번할 시에는 적합하지 않고, 주로 고정된 데이터에 대한 탐색에 적합하다.
ex 1) 10억 명이 정렬된 배열에서 이진 탐색을 이용해 특정 이름을 찾는다면 단 30번의 비교만으로 검색이 완료된다.
반면에 순차 탐색의 경우 평균 5억 번의 비교가 있어야 된다.
ex 2) 영어 사전에서 단어를 찾는 과정 역시 이진 탐색과 동일하다.
영어 사전을 펼쳐서 찾고자 하는 단어가 현재 페이지에 있는 단어보다 앞에 있는지, 뒤에 있는지를 결정한 다음,
단어가 있는 부분 만을 다시 검색한다.
이진 탐색의 구현
1. 탐색의 대상이 되는 자료들이 array[low] 에서부터 array[high]에 들어있다고 가정하자. (정렬되어 있어야 함)
즉 어떤 시점에서 탐색되어야 할 범위는 low에서 high 까지가 된다.
맨 처음 low에는 0번 인덱스의 값, high에는 n-1번 인덱스의 값이 들어갈 것이다.
2. low와 high값에 의거해 중간값 mid 값은 (low + high) / 2이다.
즉, array[low] ~ array[high] 까지의 탐색은
array[low] ~ array[middle-1] + array[middle+1] + array[high]까지의 탐색이 된다.
3. array[mid] 값과 구하고자 하는 key값을 비교한다.
3-1. key > mid : 구하고자 하는 값이 중간값보다 높다면 low를 mid +1로 만들어 줌 (왼쪽 반을 버림)
3-2. key < mid : 구하고자하는 값이 중간값 보다 낮다면 high를 mid-1로 만들어 줌 (오른쪽 반을 버림)
3-3. key == mid : 구하고자 하는 값을 찾음 중간값 리턴
4. low > high가 될 때까지 1~3번을 반복하면서 구하고자 하는 값을 찾는다.
(이때까지 못 찾으면 탐색 실패 -1, false, error 등 return)

순환 호출을 이용한 이진 탐색 구현
int binarySearch1(int key, int low, int high) {
int mid;
if(low <= high) {
mid = (low + high) / 2;
if(key == arr[mid]) { // 탐색 성공
return mid;
} else if(key < arr[mid]) {
// 왼쪽 부분 arr[0]부터 arr[mid-1]에서의 탐색
return binarySearch1(key ,low, mid-1);
} else {
// 오른쪽 부분 - arr[mid+1]부터 arr[high]에서의 탐색
return binarySearch1(key, mid+1, high);
}
}
return -1; // 탐색 실패
}반복을 이용한 이진 탐색 구현
반복 구조를 사용하는 것이 재귀 호출로 구현하는 것보다 효율적이다.
int binarySearch2(int key, int low, int high) {
int mid;
while(low <= high) {
mid = (low + high) / 2;
if(key == arr[mid]) {
return mid;
} else if(key < arr[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1; // 탐색 실패
}
전체 코드
public class BinarySearch {
static int[] arr = {1, 3, 5, 7, 8, 10, 20, 35, 99, 100};
public static void main(String[] args) {
System.out.println("1. 순환 호출을 이용한 이진 탐색");
System.out.println(binarySearch1(5, 0, arr.length-1)); // 2
System.out.println("\n2. 반복을 이용한 이진 탐색");
System.out.println(binarySearch2(20, 0, arr.length-1)); // 6
}
// 재귀적 탐색
static int binarySearch1(int key, int low, int high) {
int mid;
if(low <= high) {
mid = (low + high) / 2;
if(key == arr[mid]) { // 탐색 성공
return mid;
} else if(key < arr[mid]) {
return binarySearch1(key ,low, mid-1); // 왼쪽 부분 탐색
} else {
return binarySearch1(key, mid+1, high); // 오른쪽 부분 탐색
}
}
return -1; // 탐색 실패
}
// 반복적 탐색
static int binarySearch2(int key, int low, int high) {
int mid;
while(low <= high) {
mid = (low + high) / 2;
if(key == arr[mid]) {
return mid;
} else if(key < arr[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1; // 탐색 실패
}
}
이진 탐색의 성능
이진 탐색은 탐색을 반복할 때마다 탐색 범위를 반으로 줄인다.
이러한 탐색 범위가 더 이상 줄일 수 없는 1이 될 때의 탐색 횟수를 k라고 한다면, 아래 표와 같다.
| 비교 | 범위 |
| q0 | n |
| 1 | n/2 |
| 2 | n/4 |
| ... | ... |
| k | n/2^k |
표의 마지막 행에서 n/2^k = 1 이므로, k = log 2 n 임을 알 수 있다.
따라서 이진 탐색의 시간 복잡도는 O(log n)이 된다.
* log 2n의 경우 밑이 10인 log n으로 계산한다.
컴퓨터가 이진수 시스템을 사용하기 때문에, 로그는 밑을 대부분 2로 사용한다. (즉, log 2 n, 때때로는 log n이라고 쓰임.)
그러나, 로그의 밑이 변할 때, logan와 logbn는 오로지 상수 승수에 따라서만 달라지기에 빅-오 표기법에서는 버림 한다.
그러므로 O(log n)은 로그의 밑과 상관없이 로그 시간 알고리즘에 대한 표준 표기법이 된다.
참고
C언어로 쉽게 풀어쓴 자료구조(개정 3판) - 생능 출판
'Algorithm' 카테고리의 다른 글
| [C & Java] Heap 힙 (0) | 2021.05.19 |
|---|---|
| [Java] 다익스트라 (Dijkstra) 최단 경로 알고리즘 (402) | 2021.03.12 |
| [Java] 트리 Tree 3 - 이진 탐색 트리 (0) | 2020.12.31 |
| [Java] 트리 Tree 2 - 이진 트리의 순회(전위, 중위, 후위, 반복, 레벨) / 구현 (13) | 2020.11.06 |
| [Java] 트리(tree) 구현 - 1차원 배열 / 2차원 배열 / 클래스 3가지 방법 구현 (0) | 2020.11.05 |



댓글