1. 트리 1차원 배열로 구현

주로 포화 이진 트리나 완전 이진트리의 경우 많이 쓰이는 방법이다.
그외의 이진트리도 저장이 불가능한 것은 아니지만 기억공간의 낭비가 심해진다.
따라서 포화 이진 트리이진트리 또는 완전 이진트리를 1차원 배열로 구현해보자.
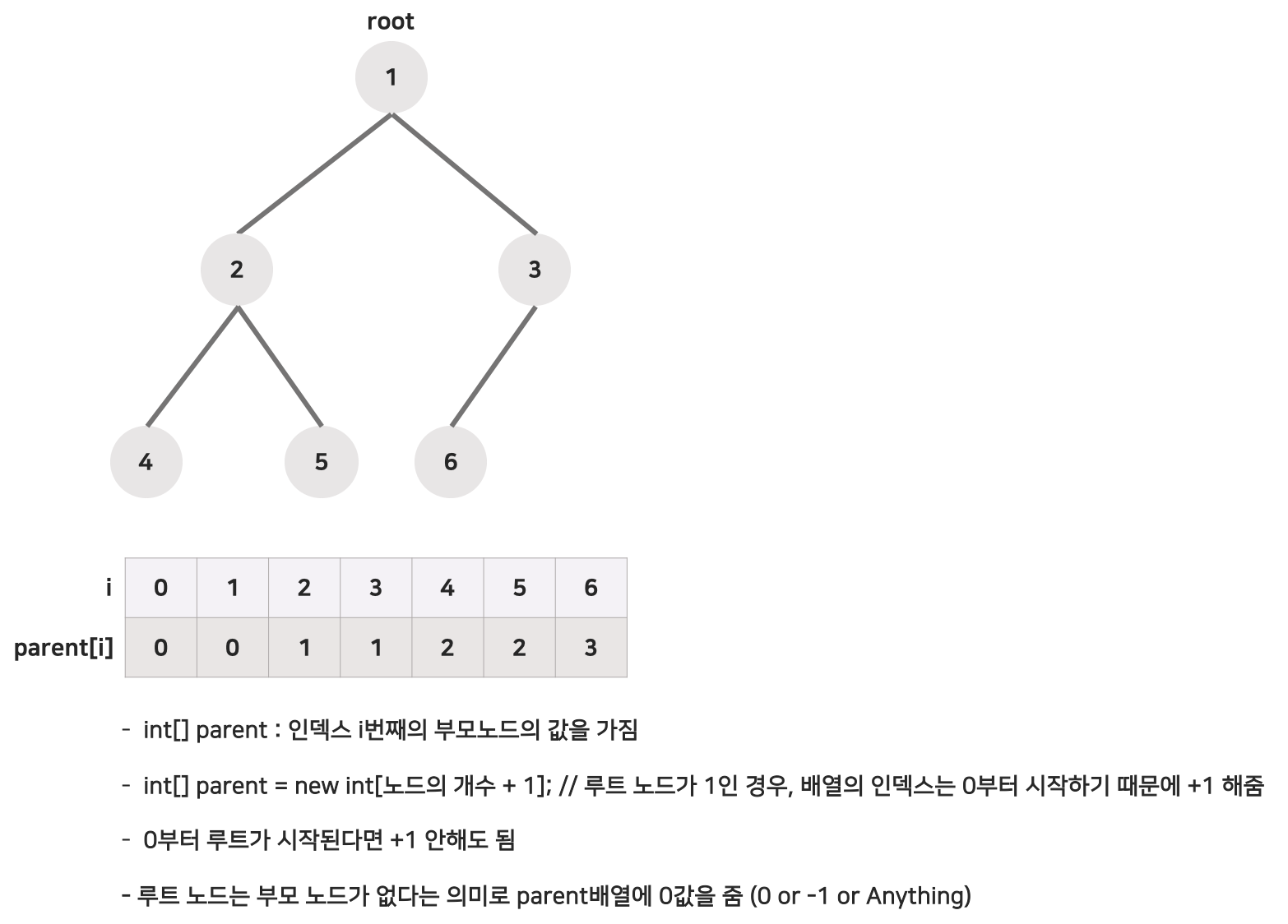
루트 노드는 1부터 시작한다.(인덱스 0은 사용하지 않는 편이 계산을 간단하게 함)
원하는 노드 n개까지 총 n+1 크기의 1차원 배열을 만든다.
그다음 이진트리의 번호대로 노드들을 저장한다.
배열 표현법에서는 인덱스만 알면 노드의 부모나 자식을 쉽게 알 수 있다.
- 노드 i의 부모 노드 인덱스 = i / 2
- 노드 i의 왼쪽 자식 인덱스 = 2i
- 노드i의 오른쪽 자식 인덱스 = 2i + 1
/**
* @author Gwon Minha
*
* 루트가 1인 완전 이진 트리, 포화 이진 트리를 1차원 배열에 저장후 각 인덱스의 부모 노드를 출력하는 프로그램
입력 : 첫 번째 줄에 트리의 노드 개수 n이 주어진다.
출력 : 각 인덱스의 부모 노드를 출력한다.
예제 : 6
1
/ \
2 3
/ \ /
3 4 5
* 포화 이진 트리이거나 완전 이진 트리이기 때문에 1차원 배열 n+1만큼 번호 순서대로 저장하면된다. (0부터라면 n까지만)
*/
import java.util.Arrays;
import java.util.Scanner;
public class Tree1Matrix {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] parent = new int[n+1]; //tree 저장을 위한 1차원 배열, 루트는 1부터 시작하기 때문에 n+1
for(int i = 2; i <= n; i++) { //1은 루트이기 때문에 2부터 시작 (tree[1] = 0)
parent[i] = i/2; //노드i의 부모 노드 인덱스 = i/2
}
System.out.println(Arrays.toString(parent));
}
}
2. 트리 2차원 배열로 구현 - 전위/중위/후위 순회 출력

/**
* @author Gwon Minha
*
* 이차원 배열로 구현한 트리의 전위, 중위, 후위 순회 결과 출력 프로그램
* 2차원 배열 [x][0] -> 노드x의 왼쪽 자식
[x][1] -> 노드x의 오른쪽 자식값을 저장하는 방식으로 트리 입력 받음
입력 : 첫 번째 줄에 트리의 노드 개수 n이 주어진다. ( 1 ≤ n ≤ 100 )
두 번째 줄부터 트리의 정보가 주어진다. 각 줄은 3개의 숫자 a, b, c로 이루어지며,
그 의미는 노드 a의 왼쪽 자식노드가 b, 오른쪽 자식노드가 c라는 뜻이다.
자식노드가 존재하지 않을 경우에는 -1이 주어진다.
출력 : 첫 번째 줄에 전위순회, 두 번째 줄에 중위순회, 세 번째 줄에 후위순회를 한 결과를 출력한다.
예제 :
6
0 1 2
1 3 4
2 -1 5
3 -1 -1
4 -1 -1
5 -1 -1
0
/ \
1 2
/ \ \
3 4 5
*/
import java.util.*;
public class TreeOrder2Matrix {
static int n;
static int[][] tree;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
tree = new int[n][2]; //tree 저장을 위한 2차원 배열
for (int i = 0; i < n; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
tree[a][0] = b; // 0은 left
tree[a][1] = c; // 1은 right
}
System.out.println("전위 순회");
preOrder(0);
System.out.println("\n중위 순회");
inOrder(0);
System.out.println("\n후위 순회");
postOrder(0);
}
//전위순회 Preorder : Root -> Left -> Right
public static void preOrder(int x) {
if (tree[x][0] == -1 && tree[x][1] == -1) { //왼쪽 자식이나 오른쪽 자식이 없다면 (-1이라면) 순회X
System.out.print(x + " ");
} else {
System.out.print(x + " ");
if (tree[x][0] != -1) {
preOrder(tree[x][0]);
}
if (tree[x][1] != -1) {
preOrder(tree[x][1]);
}
}
}
//중위 순회 Inorder : Left -> Root -> Right
public static void inOrder(int x) {
if(tree[x][0] == -1 && tree[x][1] == -1) {
System.out.print(x + " ");
} else {
if(tree[x][0] != -1) {
inOrder(tree[x][0]);
}
System.out.print(x + " ");
if(tree[x][1] != -1) {
inOrder(tree[x][1]);
}
}
}
//후위순회 Postorder : Left -> Right -> Root
public static void postOrder(int x) {
if(tree[x][0] == -1 && tree[x][1] == -1) {
System.out.print(x + " ");
} else {
if(tree[x][0] != -1) {
postOrder(tree[x][0]);
}
if(tree[x][1] != -1) {
postOrder(tree[x][1]);
}
System.out.print(x + " ");
}
}
}3. 트리 클래스 구조체로 구현 - 전위/중위/후위 순회 출력
트리를 표현할 노드가 클래스 구조체로 표현된다.
하나의 노드는 데이터를 저장하는 필드, 왼쪽 자식 노드와 오른쪽 자식 노드를 가리키는 필드 총 3개의 필드를 가진다.
-> 노드 클래스 생성
class Node { //트리의 노드 정보를 저장할 클래스 구조체
int data; //노드 값
Node left; //왼쪽 자식 노드 참조 값
Node right; //오른쪽 자식 노드 참조 값
//추가할 때 참조되는 왼쪽, 오른쪽 자식의 값은 모르닌까 일단 data 값을 기반으로 Node 객체 생성
Node(int data){
this.data = data;
}
}
본격적으로 트리를 구성하기 위해 트리 클래스를 만든다.
트리 클래스는 아래의 메서드들로 구성된다.
- 값을 추가하는 createNode() 메서드
- 값을 어느 위치에 추가할 것인지 찾기 위한 searchNode() 메서드
- 전위순회(preOrder),중위순회(inOrder), 후위 순회(postOrder) 메서드
public class TreeOrderClass {
public Node root; //초기 root는 null
public void createNode(int data, int leftData, int rightData) {
}
public void searchNode(Node node, int data, int leftData, int rightData) {
}
public void preOrder(Node node) {
}
public void preOrder(Node node) {
}
public void preOrder(Node node) {
}
}
1. 값을 추가하는 createNode() 메서드
public void createNode(int data, int leftData, int rightData) {
if(root == null) {//초기 상태 - 루트 노드 생성
root = new Node(data);
//좌우 값이 있는 경우, 즉 -1이 아닌 경우 노드 생성
if(leftData != -1) {
root.left = new Node(leftData); //왼쪽 자식 노드 값을 가지는 Node 인스턴스 생성
}
if(rightData != -1) {
root.right = new Node(rightData); //오른쪽 자식 노드 값을 가지는 Node 인스턴스 생성
}
} else { //초기 상태가 아니라면, 루트 노드 생성 이후 만들어진 노드 중 어떤건지를 찾아야함
searchNode(root, data, leftData, rightData);
}
}
트리가 생성되기 전 초기 root 값은 null이다.
트리 생성을 통해 처음 루트 노드 객체가 생성되고 왼쪽, 오른쪽 값이 있느냐 없느냐에 따라 왼쪽, 오른쪽 역시 노드 객체가 생성된다.
루트 노드 생성 이후 추가되는 노드들은 어느 위치에 추가될지 판별해야 하기 때문에 serchNode() 메서드를 통해 탐색하게 된다.
2. 값을 어느 위치에 추가할 것인지 찾기 위한searchNode() 메서드
매개변수로 들어온 node(처음엔 root 노드가 들어있음)를 시작으로 data와 같은 값을 가지는 노드를 찾는다.
찾을때까지 root노드에서부터 왼쪽, 오른쪽으로 내려간다.
찾는다면 들어갈 위치를 찾은 것임으로 왼쪽, 오른쪽 값이 있는 경우 그 노드의 왼쪽, 오른쪽 노드 객체를 생성한다.
null이라면 들어갈 위치를 찾지 못한 것임으로 재귀를 종료한다.
//매개변수로 들어온 root노드를 시작으로 data와 같은 값을 가진 node를 찾는다.
//찾을 때까지 root노드에서부터 왼쪽, 오른쪽으로 내려감
public void searchNode(Node node, int data, int leftData, int rightData) {
if(node == null) { //도착한 노드가 null이면 재귀 종료 - 찾을(삽입할) 노드 X
return;
} else if(node.data == data) { //들어갈 위치를 찾았다면
if(leftData != -1) { //.이 아니라 값이 있는 경우에만 좌우 노드 생성
node.left = new Node(leftData);
}
if(rightData != -1) {
node.right = new Node(rightData);
}
} else { //아직 찾지못했고 탐색할 노드가 남아 있다면
searchNode(node.left, data, leftData, rightData); //왼쪽 재귀 탐색
searchNode(node.right, data, leftData, rightData); //오른쪽 재귀 탐색
}
}
3. 전위 순회(preOrder), 중위 순회(inOrder), 후위 순회(postOrder) 메서드
//전위순회 Preorder : Root -> Left -> Right
public void preOrder(Node node) {
if(node != null) {
System.out.print(node.data + " ");
if(node.left != null) preOrder(node.left);
if(node.right != null) preOrder(node.right);
}
}
//중위 순회 Inorder : Left -> Root -> Right
public void inOrder(Node node) {
if(node != null) {
if(node.left != null) inOrder(node.left);
System.out.print(node.data + " ");
if(node.right != null) inOrder(node.right);
}
}
//후위순회 Postorder : Left -> Right -> Root
public void postOrder(Node node) {
if(node != null) {
if(node.left != null) postOrder(node.left);
if(node.right != null) postOrder(node.right);
System.out.print(node.data + " ");
}
}전체 코드
/**
* @author Gwon Minha
*
* 클래스로 구현한 이진 트리의 전위, 중위, 후위 순회 결과 출력 프로그램
* Class 구조체에 노드값, 왼쪽 자식 노드값, 오른쪽 자식 노드값 저장해 구현
입력 : 첫 번째 줄에 트리의 노드 개수 n이 주어진다. ( 1 ≤ n ≤ 100 )
두 번째 줄부터 트리의 정보가 주어진다. 각 줄은 3개의 숫자 a, b, c로 이루어지며,
그 의미는 노드 a의 왼쪽 자식노드가 b, 오른쪽 자식노드가 c라는 뜻이다.
자식노드가 존재하지 않을 경우에는 -1이 주어진다.
출력 : 첫 번째 줄에 전위순회, 두 번째 줄에 중위순회, 세 번째 줄에 후위순회를 한 결과를 출력한다.
예제 :
6
0 1 2
1 3 4
2 -1 5
3 -1 -1
4 -1 -1
5 -1 -1
0
/ \
1 2
/ \ \
3 4 5
*/
import java.util.*;
class Node { //트리의 노드 정보를 저장할 클래스 구조체
int data; //노드 값
Node left; //왼쪽 자식 노드 참조 값
Node right; //오른쪽 자식 노드 참조 값
//추가할 때 참조되는 왼쪽, 오른쪽 자식의 값은 모르닌까 일단 data 값을 기반으로 Node 객체 생성
Node(int data){
this.data = data;
}
}
public class TreeOrderClass {
public Node root; //초기 root는 null
public void createNode(int data, int leftData, int rightData) {
if(root == null) { //초기 상태 - 루트 노드 생성
root = new Node(data);
//좌우 값이 있는 경우, 즉 -1이 아닌 경우 노드 생성
if(leftData != -1) {
root.left = new Node(leftData); //왼쪽 자식 노드 값을 가지는 Node 인스턴스 생성
}
if(rightData != -1) {
root.right = new Node(rightData); //오른쪽 자식 노드 값을 가지는 Node 인스턴스 생성
}
} else { //초기 상태가 아니라면, 루트 노드 생성 이후 만들어진 노드 중 어떤건지를 찾아야함
searchNode(root, data, leftData, rightData);
}
}
//매개변수로 들어온 root노드를 시작으로 data와 같은 값을 가진 node를 찾는다.
//찾을 때까지 root노드에서부터 왼쪽, 오른쪽으로 내려감
public void searchNode(Node node, int data, int leftData, int rightData) {
if(node == null) { //도착한 노드가 null이면 재귀 종료 - 찾을(삽입할) 노드 X
return;
} else if(node.data == data) { //들어갈 위치를 찾았다면
if(leftData != -1) { //-1이 아니라 값이 있는 경우에만 좌우 노드 생성
node.left = new Node(leftData);
}
if(rightData != -1) {
node.right = new Node(rightData);
}
} else { //아직 찾지못했고 탐색할 노드가 남아 있다면
searchNode(node.left, data, leftData, rightData); //왼쪽 재귀 탐색
searchNode(node.right, data, leftData, rightData); //오른쪽 재귀 탐색
}
}
//전위순회 Preorder : Root -> Left -> Right
public void preOrder(Node node) {
if(node != null) {
System.out.print(node.data + " ");
if(node.left != null) preOrder(node.left);
if(node.right != null) preOrder(node.right);
}
}
//중위 순회 Inorder : Left -> Root -> Right
public void inOrder(Node node) {
if(node != null) {
if(node.left != null) inOrder(node.left);
System.out.print(node.data + " ");
if(node.right != null) inOrder(node.right);
}
}
//후위순회 Postorder : Left -> Right -> Root
public void postOrder(Node node) {
if(node != null) {
if(node.left != null) postOrder(node.left);
if(node.right != null) postOrder(node.right);
System.out.print(node.data + " ");
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
TreeOrderClass t = new TreeOrderClass();
for (int i = 0; i < n; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
t.createNode(a, b, c);
}
System.out.println("전위 순회");
t.preOrder(t.root);
System.out.println("\n중위 순회");
t.inOrder(t.root);
System.out.println("\n후위 순회");
t.postOrder(t.root);
}
}연습 문제
관련 포스트
[C & Java] 트리 Tree 1 - 트리? / 이진트리? / 트리 표현법
[Java] 트리(tree) 구현 - 1차원 배열 / 2차원 배열 / 클래스 3가지 방법 구현
[Java] 트리 Tree 2 - 이진트리의 순회(전위, 중위, 후위, 반복, 레벨) / 구현
[Java] 트리 Tree 3 - 이진 탐색 트리
GITHUB
github.com/KwonMinha/Algorithm/tree/master/Tree/src
KwonMinha/Algorithm
Contribute to KwonMinha/Algorithm development by creating an account on GitHub.
github.com
'Algorithm' 카테고리의 다른 글
| [Java] 트리 Tree 3 - 이진 탐색 트리 (0) | 2020.12.31 |
|---|---|
| [Java] 트리 Tree 2 - 이진 트리의 순회(전위, 중위, 후위, 반복, 레벨) / 구현 (13) | 2020.11.06 |
| [C & Java] 트리 Tree 1 - 트리? / 이진트리? / 트리 표현법 (0) | 2020.11.03 |
| [Java] DFS로 모든 이동 경로 구하기 (0) | 2020.09.23 |
| [Java] 조합 Combination (6) | 2020.05.12 |




댓글